简介
推荐在学习的过程中,放慢速度,比如一天只学一章,尽量将demo中的代码实现下。
在技术圈,我们经常喜欢谈论高大上的架构,比如高可用、微服务、服务治理等等。鲜有人关注代码层面的编程能力,愿意沉下心来花几个月时间啃一啃计算机基础知识,认认真真夯实基础。PS:笔者在学习区块链时,区块链的原理很快就搞懂了,但真要说操盘一个项目还是远远不敢想的,因为面对具体的业务场景,不知道如何将取舍映射到技术上,也就始终跟区块链隔着距离。
像《算法导论》这些经典书籍,虽然很全面,但是过于理论,缺乏真实的开发场景,学起来非常枯燥,过不了几天就忘了。PS:计算机专业都会教《数据库原理》,讲了数据库的历史、三大范式、组成、事务等等,但你最直观的工作感受是什么?数据库压力很大怎么办。所以,描述一个知识有两种方式,一种是how、what、when、why等娓娓道来;一种是拿一个问题将所有的知识点串起来。
人生路上,我们会遇到很多的坎儿。跨过去,你就可以成长,跨不过去就是困难和停滞。而在后面很长一段时间里, 你都需要为这个困难买单。
为什么要学习数据结构和算法
学习的重点:
- 复杂度分析,作者将这个事儿提到了一个极其重要的高度
- 除了知识本身外,更重要的是它的来历、特点和应用场景
算法的复杂度,
- 多项式量级,O(1),O(n),O(n^2),O(logn),O(nlogn)
- 非多项式量级,只有两个:O(2^n)和O(n!),这类问题称为NP问题。
考虑一下场景:
- 向数组第k个位置插入一个元素。将第k个原有的元素挪到数组最后
- 从数组中删除一个元素。将该位置标记为已删除,然后在一个时刻统一删除。想想jvm的标记清理算法
- 基于数组实现一个队列
为什么很多人的第一个反应是移动元素?原因就是
- 很多人没有将数组 作为存储结构,而是逻辑结构。作为逻辑结构的数组,它的定义是:用一组连续的内存空间,来存储一组具有相同类型的数据。作为存储结构,这就是一段儿空间,爱连续不连续。作为逻辑结构,就必须保持它的连续性。
- 我们在说问题的时候,没有说业务场景。如果我跟你说jvm垃圾清理,你肯定知道标记清除算法,无需在每一个时刻都保持数组数据的“纯洁性”。
- X/Y 问题。将元素插入数组的第K个位置,并没有说要维持数组原来的数据顺序。
时间复杂度代表的是一个增长趋势,但是,我们前面讲过,在大 O 复杂度表示法中,我们会省略低阶、系数和常数,也就是说,O(nlogn) 在没有省略低阶、系数、常数之前可能是 O(knlogn + c),而且 k 和 c有可能还是一个比较大的数。(尤其是k、c远大于n的时候),比如对于小规模数据的排序,O(n2) 的排序算法并不一定比 O(nlogn) 排序算法执行的时间长。对于小数据量的排序,我们选择比较简单、不需要递归的插入排序算法。
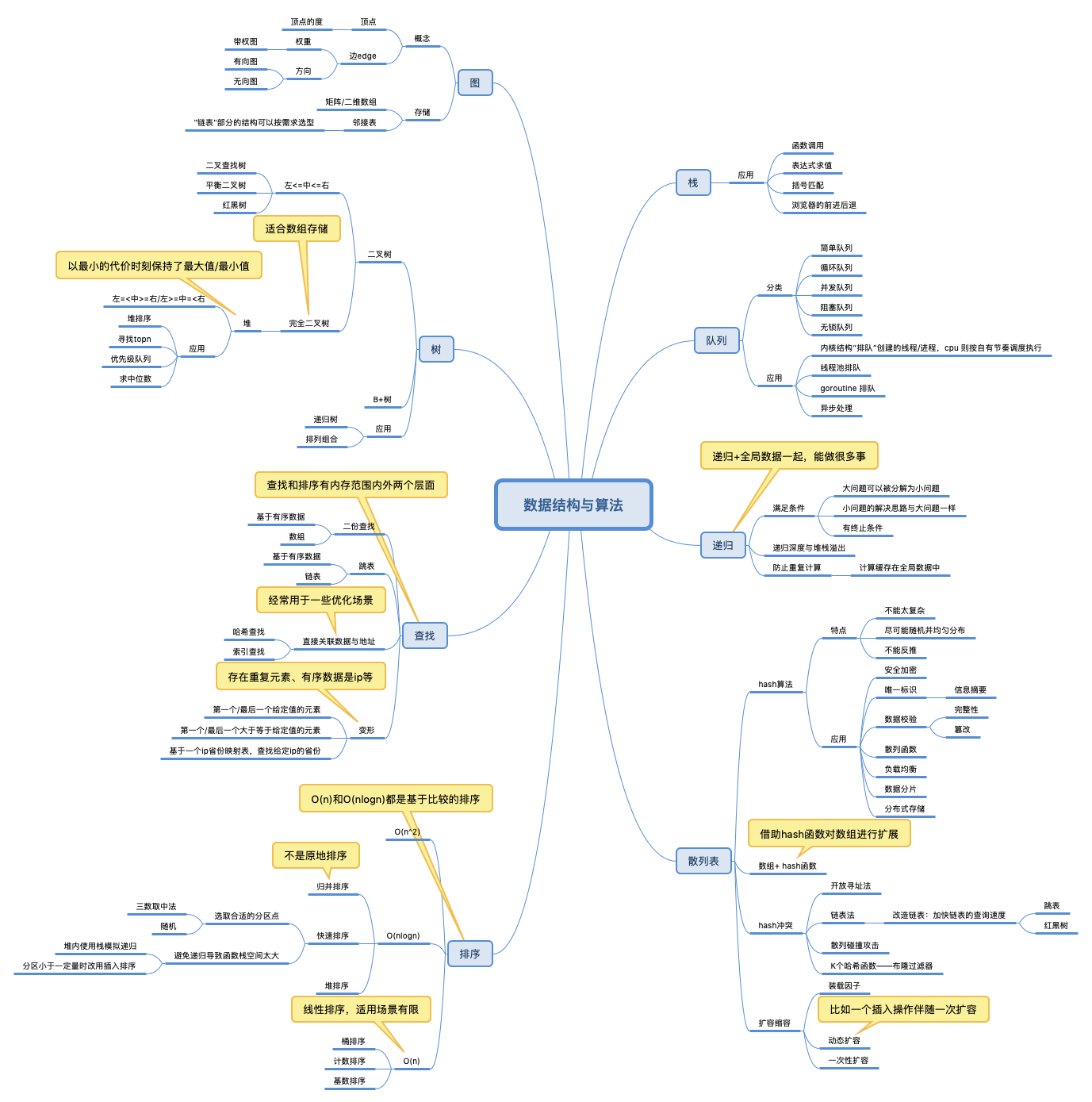
常用的数据结构
栈在函数调用中的应用,一次回收一个数据意思不大,但一次回收一个栈帧,即可实现返回值、参数、局部变量的自动分配与回收。cpu 栈寄存器 + 出入栈指令 这类硬件支持,加上栈操作形式的相对固定,使得编译器层面便可以屏蔽这些细节。甚至反过来说,是硬件特性 + 编译器 造就了“方法/函数”这一抽象,而不是方法利用了栈的特性。jvm 虽说堆内存垃圾回收很高端,但这类复杂的事儿就只能语言的虚拟机层 解决了。
常用算法
- 数组 + 哈希函数 就成了一个散列表。 对于跳表来说,与其说数据结构本来就是那样子,还不如说为了在链表上提高查询速度而衍生的数据结构。对于B+树,换个角度想,我们可以说先有底层那一条叶子链,再有的上层索引结构。
- 阐述了为什么查询和排序是基本的算法,以及教程中提到的为什么散列表经常和链表一起使用。
链表:和数组一样,链表也可以是多维的
排序
快排伪代码
// 快速排序,A 是数组,n 表示数组的大小
quick_sort(A, n) {
quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数,p,r 为下标
quick_sort_c(A, p, r) {
if p >= rthen return
q = partition(A, p, r) // 获取分区点
quick_sort_ck_sort_c(A, p, q-1)
quick_sort_c(A, q+1, r)
}
如果我们不考虑空间消耗的话,partition() 分区函数可以写得非常简单。我们申请两个临时数组 X 和 Y,遍历 A[p…r],将小于 pivot 的元素都拷贝到临时数组 X,将大于 pivot 的元素都拷贝到临时数组 Y,最后再将数组X 和数组 Y 中数据顺序拷贝到 A[p…r]。PS:这种表述方式让笔者对快排更有感觉了。
随机选择一个元素做“轴元素”,将所有大于轴元素的移到左边,其余移到右边。关键就是:从这一刻开始,小于“轴元素”的那些数就再也没有机会与大于“轴元素”的数进行两两比较了。
排序的本质可以这样来表述:一组未排序的N个数字,它们一共有N!种重排,其中只有一种排列是满足题意的。将排序问题看成和猜数字(给一定范围,猜测提问者写好的数字)一样,是通过问问题来缩小/排除(narrow down)结果的可能性区间,这样一来,就会发现,“最好的问题”就是那些能够均分所有可能性的问题,因为那样的话不管问题的答案如何,都能排除掉k-1/k(k为问题的答案有多少种输出——猜数字里面是2,称球里面是3)种可能性,而不均衡的问题总会有一个或一些答案分支排除掉的可能性要小于k-1/k。于是策略的下界就被拖累了。
哈希/分治和归并
哈希算法的定义和原理非常简单,基本上一句话就可以概括了:将任意长度的二进制值串映射为固定长度的二进制值串。后者就有很多的意涵了:
- 可以视为源数据的特征/标识/摘要
- 可以是分桶的桶号
- 可以是为了掩盖源数据或防篡改(安全加密)
归并排序和快速排序都是分治,但比较好玩的是
- 归并排序是简单的缩小数据规模,或者可以认为是根据数据位置将数据集两两划分。
- 快速排序是根据数据特征来将数据集两两划分。
假如我们有 1T 的日志文件,这里面记录了用户的搜索关键词,我们想要快速统计出每个关键词被搜索的次数,该怎么做呢?
- 首先就是分治,将数据规模缩小到单机可以处理的程度
- 分治就涉及到怎么分的问题?肯定是“快排”的分法更好一些,快排(从小到大)保证了左边整体一定比右边小,将快排的“二分”扩散成“多分”, 同一个搜索关键词按哈希(哈希也是数据特征的一种)被分配到同一个机器上
那么分治后的结果如何归并呢?
- 不需要归并,比如上例的统计搜索关键词次数
- 大文件排序的归并,堆合并
树
基于数学图论中的各种模型,例如各种二叉树、多叉树、有向图和无向图等等。通常,这些模型表示了顶点和顶点之间的稀疏关系,所以它们常常是基于指针或者对象引用来实现的。
树的划分方式有很多
- 一个是结构的限定,比如分几叉
- 一个是内容的限定,比如节点大小必须左<中<右
二叉树既可以用链式存储,也可以用数组顺序存储。数组顺序存储的方式比较适合完全二叉树,其他类型的二叉树用数组存储会比较浪费存储空间。
二叉查找树,二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。进而带来几个特性:中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n)
支持重复数据的二叉查找树,如何处理重复数据:
- 二叉查找树中每一个节点不只存储数据,还挂一个链表或支持动态扩容的数组等数据结构,把值相同的数据都存储在同一个节点上。恍惚之间跟hashmap异曲同工。数据结构保存的是数据和数据的关系,数组只是保存数据关系的方式之一。
- 将这个要插入的数据放到等值节点的右子树
二叉树的演化逻辑
平衡二叉树:二叉树中任意一个节点的左右子树的高度相差不能大于 1。发明平衡二叉查找树这类数据结构的初衷是,解决普通二叉查找树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化的问题。
AVL 树是一种高度平衡的二叉树,所以查找的效率非常高,但是有利就有弊,AVL 树为了维持这种高度的平衡,就要付出更多的代价。每次插入、删除都要做调整,就比较复杂、耗时。那对于频繁插入、删除的场合,如何减少调整呢?
- 删除的时候只是标记删除,但不真正删除
- 一个节点存储更多的数据(更多的分叉),就减少了左旋、右旋的次数。比如mysql innodb的索引树,一个节点的数据大小直接是一个内存块。以2-3树为例从2-3-4树谈到Red-Black Tree(红黑树)
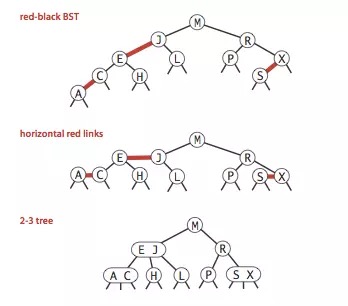
Left-Leaning Red-Black Trees2-3-4 树在多数编程语言中实现起来相对困难,因为在树上的操作涉及大量的特殊情况。红黑树实现起来更简单一些,所以可以用它来替代。红黑树与2-3-4树的等价性:2-3-4树最终能转换成一棵红黑树,反过来对于红黑树,将红链接相连的节点合并,得到的就是一颗2-3树。
红黑树只是做到了近似平衡,并不是严格的平衡,所以在维护平衡的成本上,要比 AVL 树要低。

堆
要实现一个堆,我们先要知道,堆都支持哪些操作以及如何存储一个堆。这句话体现的思维方式很重要,你设计一个系统,也要分析用户对这个系统有哪些操作系统设计的一些体会
堆的结构通过最小的代价时刻对外保持最大值或最小值。堆是完全二叉树,可用数组存储,一样是数组存储,但不是按序插入/删除,便可以使得第一个元素永远是最大/小值,其它部分依然是无序的(当然堆的上层都比下层大,也不能说是完全无序)。不讲堆排序,单单是建堆的话,完全无序 ==> 最大/小值 + 其它部分无序 ==> 完全有序。这个特性
- 你用一部分就是topk
- 你全用就是排序
-
如果最大值 指的不是元素本身,而是元素附带的优先级的话, 便是一个优先级队列
- 队列的两个基本操作:push和poll
- 优先级队列的两个基本操作:push和pull优先级最高的元素
- 你用一半就是中位数(你要证明一半数比它小,一半数比它大),即用一个数组的一半元素建个大顶堆,另一半建一个小顶堆(所有元素都比大顶堆大),那么大顶堆堆顶一定是中位数。它的一个变形是 求 99 百分位数据(比如监控系统的99%响应时间)
图
| 数组 | 链表 | 存储效率 | |
|---|---|---|---|
| 线性表 | 链表略差 | ||
| 树 | 节点间关系通过位置表示 | x叉树 | 不是“完全的”树时数组较差 |
| 图 | 二维数组/邻接矩阵 | 邻接表 | 稀疏矩阵时数组较差 |
总的来说,相对数组,链表的方式对计算机缓存命中不友好。
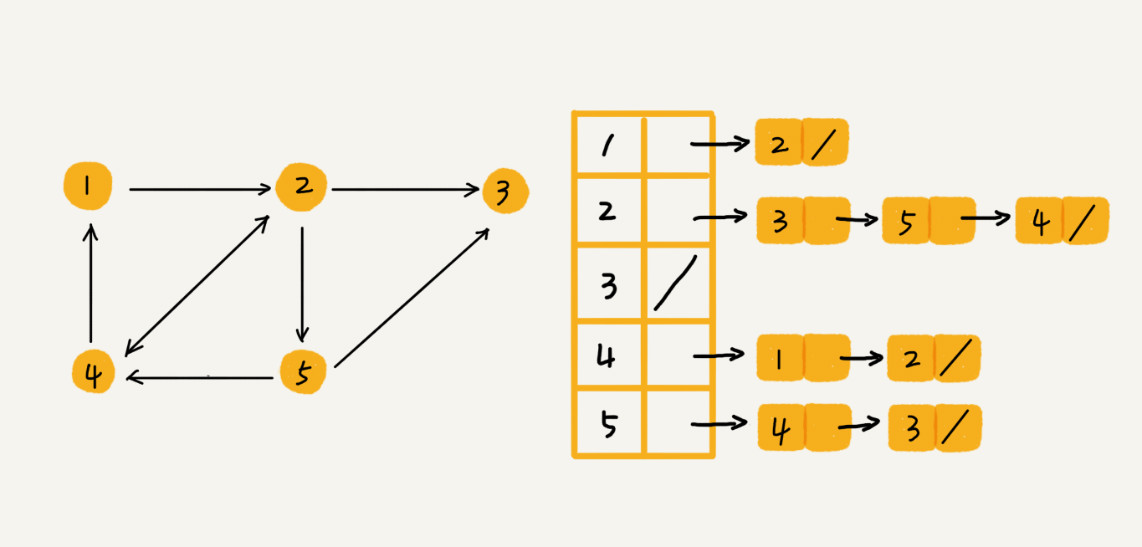
邻接表乍一看还有点像散列表,在基于链表法解决冲突的散列表中,如果链过长,为了提高查找效率,我们可以将链表换成其他更加高效的数据结构,比如平衡二叉查找树、红黑树、跳表等,邻接表同理。数据结构是为算法服务的,所以具体选择哪种存储方法,与期望支持的操作有关系。比如我们假设微博使用图来存储好友关注关系,需要分页返回粉丝列表,邻接表中的链表就可以使用跳表,因为跳表的数据本来就是有序的。如果只有几十万用户,社交关系可以存在内存中,若是上亿用户,则可以把邻接表存储在不同的机器上。
邻接表链表方案的选择 是一个直观的“兵无定式,水无常形”。妹子说喜欢吃“麻婆豆腐”犯不着没有麻婆豆腐就不点菜了,麻的、辣的、豆腐都可以点。我们看到邻接表教科书上用的链表,也不是就定死了不能换其它结构,实际上无所谓是链表、数组、红黑树、跳表。“链表”部分用什么结构“无定式”,“定式”是操作需求。
从这个角度再来看,为什么很多书花很多篇幅将查找和排序?因为很多需求最终都可以归结为查找和排序,然后才是,在极致的查找、排序效率亦或者两者平衡的数据结构之间选择。数据结构就像是设计模式,不是为了用设计模式而用设计模式,而是你知道这应该有一个事件通知的设计,然后才是去应用一个观察者模式。
索引的门道
索引真是个好东西。索引的英文名字叫:index,这个英文单词让我们联想到什么?在实际的编程中,index这个单词真是到处可见。例如:数组的下标就是index。计算机大部分工作都是在Addressing,所以,在计算机中,索引到处存在。小到操作系统虚拟内存到真实内存的映射,就是索引嘛,大到分布式系统、网络,都是这个原理。
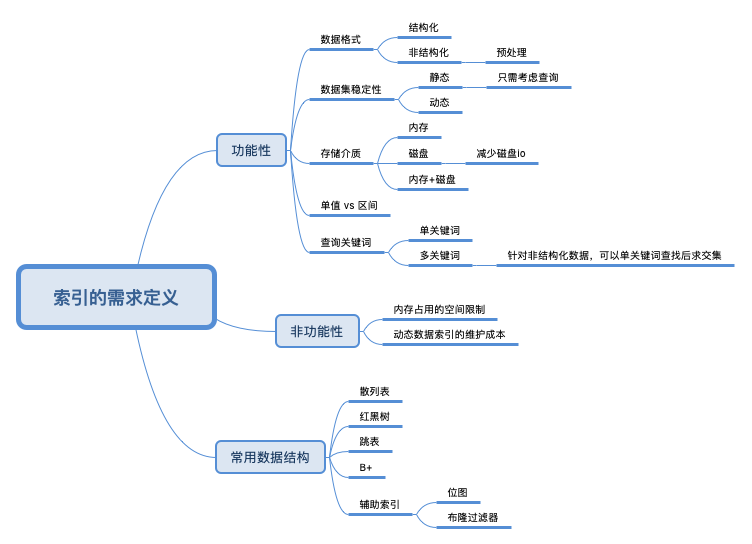
小结
学习数据结构最难的不是理解和掌握原理,而是能灵活地将各种场景和问题抽象成对应的数据结构和算法。
知识的学习是一个反复迭代、不断沉淀的过程
该教程的几个很大的意义
- 重新组织了数据结构的知识,比如数据结构课本上的查找只说了一个(基于数组的)二分查找。而教程在“查找”章节 讲了 基于链表的查询的跳表。笔者在最开始接触跳表时,则没有将两者联系在一起。联系在一起有什么好处呢?“基于有序链表的查找”便是对跳表信息量的 降维。
- 为很多结构找到工程上实际的例子,比如图与微博好友关注业务的关联,再引出不同的业务需求对图实现结构的影响。
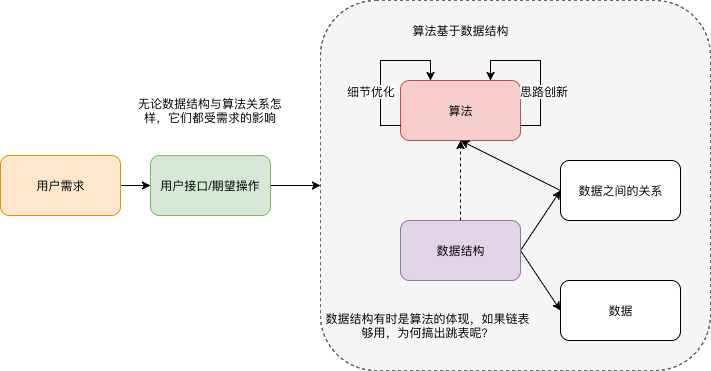
从系统设计和业务设计中来看待数据结构的话,我们一般从需求出发,先提炼“用户接口”,已有的结构 一般只能满足简单的信息存储需求, 对于其它需求则需添加辅助存储结构 或者根本上改变存储结构。如果一些“用户接口” 怎么实现都纠结,则通常意味着 信息不够,以笔者现在的经验看,这些信息一般意味着一些中间状态。中间状态(在内存中)或许不需要存储到db,但对于特定接口很有必要。
算法一般作用于特定的数据结构之上,比如二分查找是基于数组的,在链表上就玩不转了。
情商比智商更重要,而情商中最重要的,我觉得就是逆商(逆境商数,Adversity Quotient),也就是,当你遇到困难时,你会如何去面对,这将会决定你的人生最终能够走多远。
如果单单是存储数据,可以用线性表。若是存储数据间略微复杂的关系,便要用到树和图。不存复杂关系,但要兼顾对数据各种操作的性能,也要用树等结构。熵的概念
个人微信订阅号
